1. Objective
  2. Gali (1999) model:
    • Data preparation
    • Model Specification
    • Estimation of the VAR
    • Validation of the VAR
  3. VAR in reduced form (uses):
    • Granger causality
    • Forecasting
  4. VMA representation
    • Obtaining the VMA with R
  5. Uses of VAR: “structural” analysis:
    • IRFs
    • FEVD



1. Objective


  • Lab to illustrate the possibilities of VAR modelling with R

  • We are going to use the R package vars written by Bernhard Pfaff. A short description of the functionalities of the Pfaff’s package could be found here. For a more detailed exposition, please go here

  • To illustrate the different topics in VAR modelling, we are going to use as an example the analysis and data used in Gali (1999) paper : "Technology, Employment, and the Business Cycle: Do Technology Shocks Explain Aggregate Fluctuations?


2. Gali (1999) model


  • In his paper, Gali estimates a bivariate VAR with productivity and hours to look mainly at the response of hours to a technology shock

  • In fact we are going to “replicate” the Gali paper but only his benchmark model:

    • U.S. quarterly data for 1948:1 - 1994:4 from Citibase

    • bivariate VAR model: productivity(\(x_{t}\)) and hours(\(n_{t}\))

    • \(y_{t~}=~\left[ x_{t~},n_{t}\right] ^{^{\prime }}\), both variables in (log) first differences


To replicate in your PC the Gali analysis, copy and paste the following R script:

  • Be aware that you have to change the path to load the data. The DATA_gali_99.csv file with the data are in Aula virtual


Data preparation


Step by step the analysis will be:

  • Let’s start opening R and loading the Gali(99) data. The original data can be found at the Estima web page (on the file galiaer1999.zip)


  • Let’s see what variables are inside the data file
'data.frame':   192 obs. of  8 variables:
 $ GDPQ : num  1240 1247 1255 1270 1284 ...
 $ LHEM : num  NA NA NA NA 57976 ...
 $ LPMHU: num  91.7 91.4 91.6 92.9 93.3 ...
 $ P16  : num  101203 101662 102060 102386 102691 ...
 $ FM2  : num  NA NA NA NA NA NA NA NA NA NA ...
 $ FYGM3: num  0.38 0.38 0.737 0.907 0.99 ...
 $ PUNEW: num  21.7 22 22.5 23.1 23.6 ...
 $ CANN : num  NA NA NA NA NA NA NA NA NA NA ...


  • The data are quarterly and runs from 1947:1 to 1994:4

  • The vars package only works with data in a specific format: time series or ts. To convert our data in the time series format we are going to use the ts() function in R

    • GDPQ is the measure of aggregate output

    • LPMHU is labor input (hours)


  • We will start the analysis with the sample 1948:1 to 1994:4


  • Finally, the two variables used in the Gali’s VAR were dx and dy: first difference of productivity and hours (both in logs) [growth rate’s of labor productivity (dx) and hours (dn)]

  • That is, Hours and Productivity are supposed to be I(1) variables. Obviously, Gali checked this before

  • The VAR is estimated using data from 1948:1 - 1994:4 for the variables dx dn


  • To estimate the VAR models we are going to use the R vars package, let’s load the vars package


  • We are now ready to estimate the VAR model: the vars package has a function, the VAR() function, that estimate VAR models by OLS

  • Simply writing in the R console the following: VAR(variables, p = 4, type = "const"), we will estimate a VAR model for the 2 variables in the matrix called “variables” with a constant and 4 lags(p), … but, why 4 lags?


  • How p should be fixed? How to select the order of the VAR model?


Model Specification

We have already decided which variables to include in our VAR model, the sample, if the variables are I(1) vs. I(0) , and the deterministic components . In this case we have almost finished the model specification. Almost, because … we need to decide the order of the VAR.


How to select (p) the order of the VAR?

For a more detailed exposition go to Lütkepohl(2011), pp. 10-11

  • The idea is that we have to select an order(p) sufficiently large to ensure that the residuals shown no autocorrelation but without exhausting the degrees of freedom.

  • The order of the VAR could be selected by:

    1. Sequential testing procedures

    2. Model selection criteria

  • The package “vars” has the VARselect() function that allows to apply easily the 2nd approach to select p.

  • Remember that for viewing the syntax and options of an R function you could use the R args() function

  • If you need additional explanations you should call the R-help typing at the R console the following: ?VARselect


function (y, lag.max = 10, type = c("const", "trend", "both", 
    "none"), season = NULL, exogen = NULL) 
NULL
$selection
AIC(n)  HQ(n)  SC(n) FPE(n) 
     2      2      1      2 

$criteria
                1          2          3          4         5          6
AIC(n) -1.5849704 -1.6556248 -1.6258129 -1.6125929 -1.612723 -1.6200352
HQ(n)  -1.5416478 -1.5834204 -1.5247267 -1.4826249 -1.453873 -1.4323036
SC(n)  -1.4781307 -1.4775586 -1.3765202 -1.2920736 -1.220977 -1.1570629
FPE(n)  0.2049551  0.1909782  0.1967674  0.1994038  0.199406  0.1979932
                7          8
AIC(n) -1.6087278 -1.5938218
HQ(n)  -1.3921144 -1.3483267
SC(n)  -1.0745290 -0.9883966
FPE(n)  0.2002998  0.2033812


  • Three criteria (AIC,HQ &FPE) choose p=2; BUT, as our data are quarterly, probably, as Gali does, a more sensible choice would be p=4


Finally, we are now ready to estimate our VAR with p=4. Let’s go!!!


Estimation of the VAR


  • Estimating the VAR model (in reduced form)


  • Let’s see the estimation results. The best way is through the function summary()

VAR Estimation Results:
========================= 
Endogenous variables: dx, dn 
Deterministic variables: const 
Sample size: 183 
Log Likelihood: -361.495 
Roots of the characteristic polynomial:
0.7609 0.7609 0.4955 0.4955 0.4125 0.3886 0.3886 0.04377
Call:
VAR(y = variables, p = 4, type = "const")


Estimation results for equation dx: 
=================================== 
dx = dx.l1 + dn.l1 + dx.l2 + dn.l2 + dx.l3 + dn.l3 + dx.l4 + dn.l4 + const 

       Estimate Std. Error t value Pr(>|t|)    
dx.l1 -0.096398   0.076313  -1.263   0.2082    
dn.l1 -0.118188   0.075043  -1.575   0.1171    
dx.l2  0.175137   0.078470   2.232   0.0269 *  
dn.l2 -0.231832   0.092432  -2.508   0.0131 *  
dx.l3  0.032485   0.076911   0.422   0.6733    
dn.l3  0.114524   0.092560   1.237   0.2176    
dx.l4  0.009445   0.076295   0.124   0.9016    
dn.l4 -0.016682   0.076980  -0.217   0.8287    
const  0.389255   0.083809   4.645  6.7e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 0.6734 on 174 degrees of freedom
Multiple R-Squared: 0.1575, Adjusted R-squared: 0.1187 
F-statistic: 4.065 on 8 and 174 DF,  p-value: 0.0001858 


Estimation results for equation dn: 
=================================== 
dn = dx.l1 + dn.l1 + dx.l2 + dn.l2 + dx.l3 + dn.l3 + dx.l4 + dn.l4 + const 

      Estimate Std. Error t value Pr(>|t|)    
dx.l1  0.30492    0.07547   4.040    8e-05 ***
dn.l1  0.71481    0.07422   9.631   <2e-16 ***
dx.l2  0.05422    0.07761   0.699   0.4857    
dn.l2 -0.12814    0.09142  -1.402   0.1628    
dx.l3  0.02442    0.07607   0.321   0.7485    
dn.l3  0.10069    0.09154   1.100   0.2729    
dx.l4  0.05498    0.07546   0.729   0.4672    
dn.l4 -0.13815    0.07613  -1.815   0.0713 .  
const  0.07376    0.08289   0.890   0.3748    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 0.666 on 174 degrees of freedom
Multiple R-Squared: 0.4759, Adjusted R-squared: 0.4518 
F-statistic: 19.75 on 8 and 174 DF,  p-value: < 2.2e-16 



Covariance matrix of residuals:
         dx       dn
dx  0.45344 -0.06341
dn -0.06341  0.44351

Correlation matrix of residuals:
        dx      dn
dx  1.0000 -0.1414
dn -0.1414  1.0000


  • Let’s see the (same) estimation results, but in other format: the \(A_{i}\) matrices
[[1]]
         dx.l1      dn.l1
dx -0.09639832 -0.1181884
dn  0.30492251  0.7148050

[[2]]
       dx.l2      dn.l2
dx 0.1751366 -0.2318322
dn 0.0542222 -0.1281375

[[3]]
        dx.l3     dn.l3
dx 0.03248468 0.1145240
dn 0.02442320 0.1006887

[[4]]
         dx.l4       dn.l4
dx 0.009444778 -0.01668181
dn 0.054984423 -0.13815029


  • After estimation and before to use or transform our VAR we have to check their validity, mainly looking at the residuals



Validation of the VAR


  1. Stability and roots


[1] 0.76092599 0.76092599 0.49550808 0.49550808 0.41252822 0.38858444 0.38858444
[8] 0.04376503


  1. Accessing the Y-fitted, with the fitted() function


         dx         dn
1 1.0117163 -0.6248601
2 1.0254013 -0.5451213
3 0.7838393  0.1710223
4 0.9547305 -0.2437604


  1. Accessing the residuals


          dx         dn
1  0.3374632 -0.9774587
2  0.8121841 -0.4816300
3 -0.4217890 -1.3515856
4  1.6152363  1.3684236


  1. “Plotting” our VAR



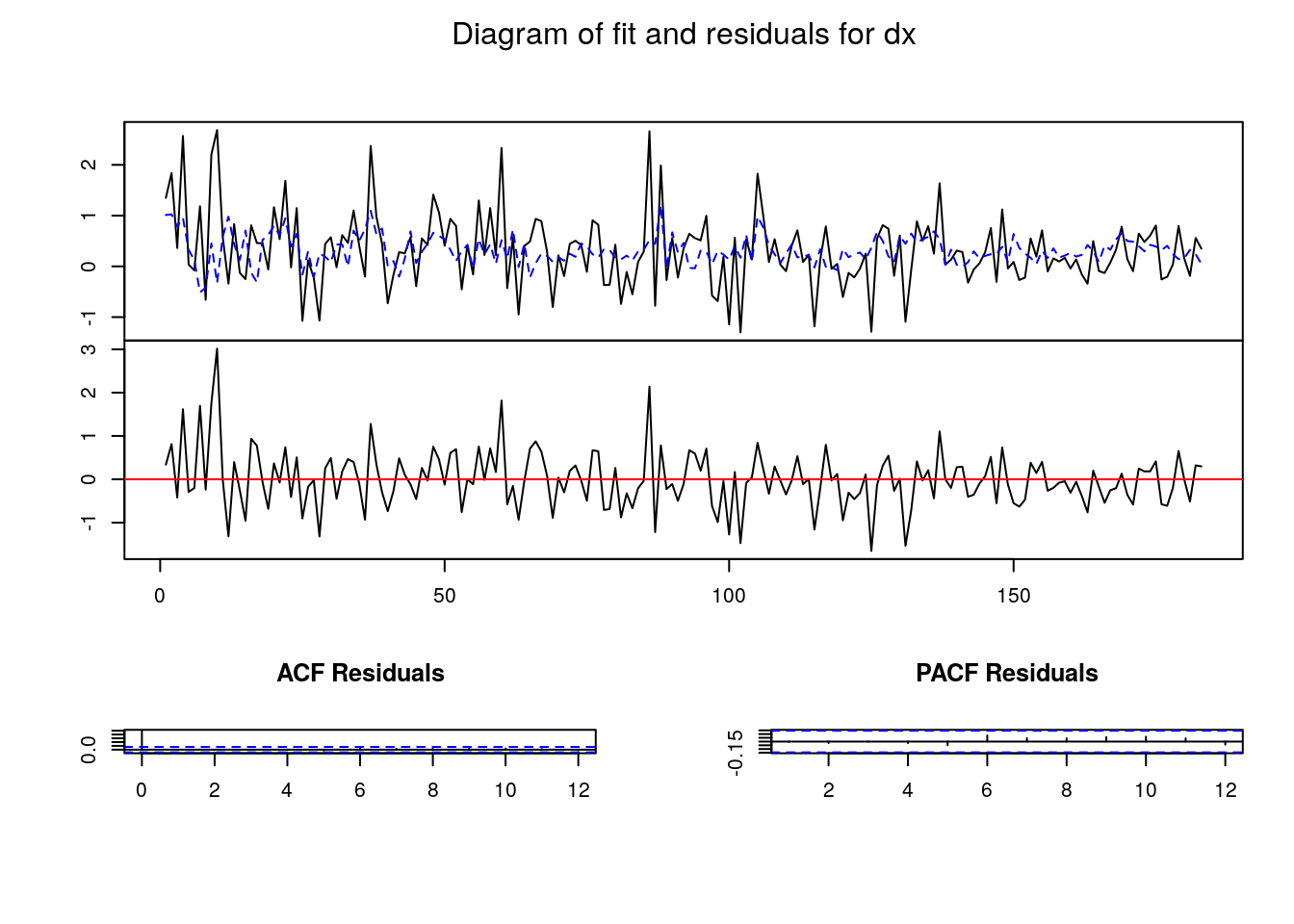
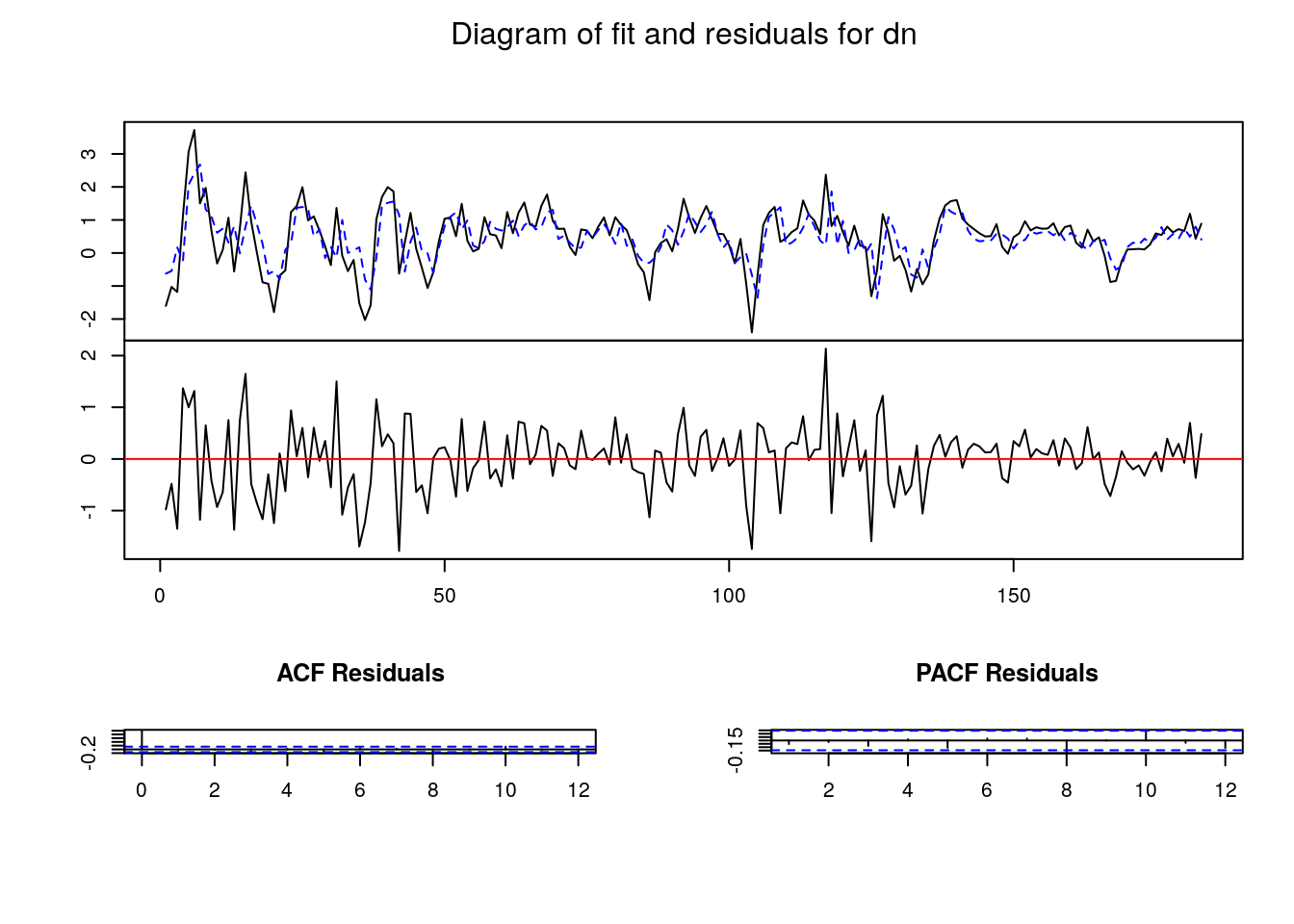
  1. Testing on the residuals



    Portmanteau Test (asymptotic)

data:  Residuals of VAR object our_var
Chi-squared = 24.955, df = 16, p-value = 0.07061
$dx

    JB-Test (univariate)

data:  Residual of dx equation
Chi-squared = 68.644, df = 2, p-value = 1.221e-15


$dn

    JB-Test (univariate)

data:  Residual of dn equation
Chi-squared = 3.6281, df = 2, p-value = 0.163


$JB

    JB-Test (multivariate)

data:  Residuals of VAR object our_var
Chi-squared = 75.873, df = 4, p-value = 1.332e-15


$Skewness

    Skewness only (multivariate)

data:  Residuals of VAR object our_var
Chi-squared = 16.763, df = 2, p-value = 0.000229


$Kurtosis

    Kurtosis only (multivariate)

data:  Residuals of VAR object our_var
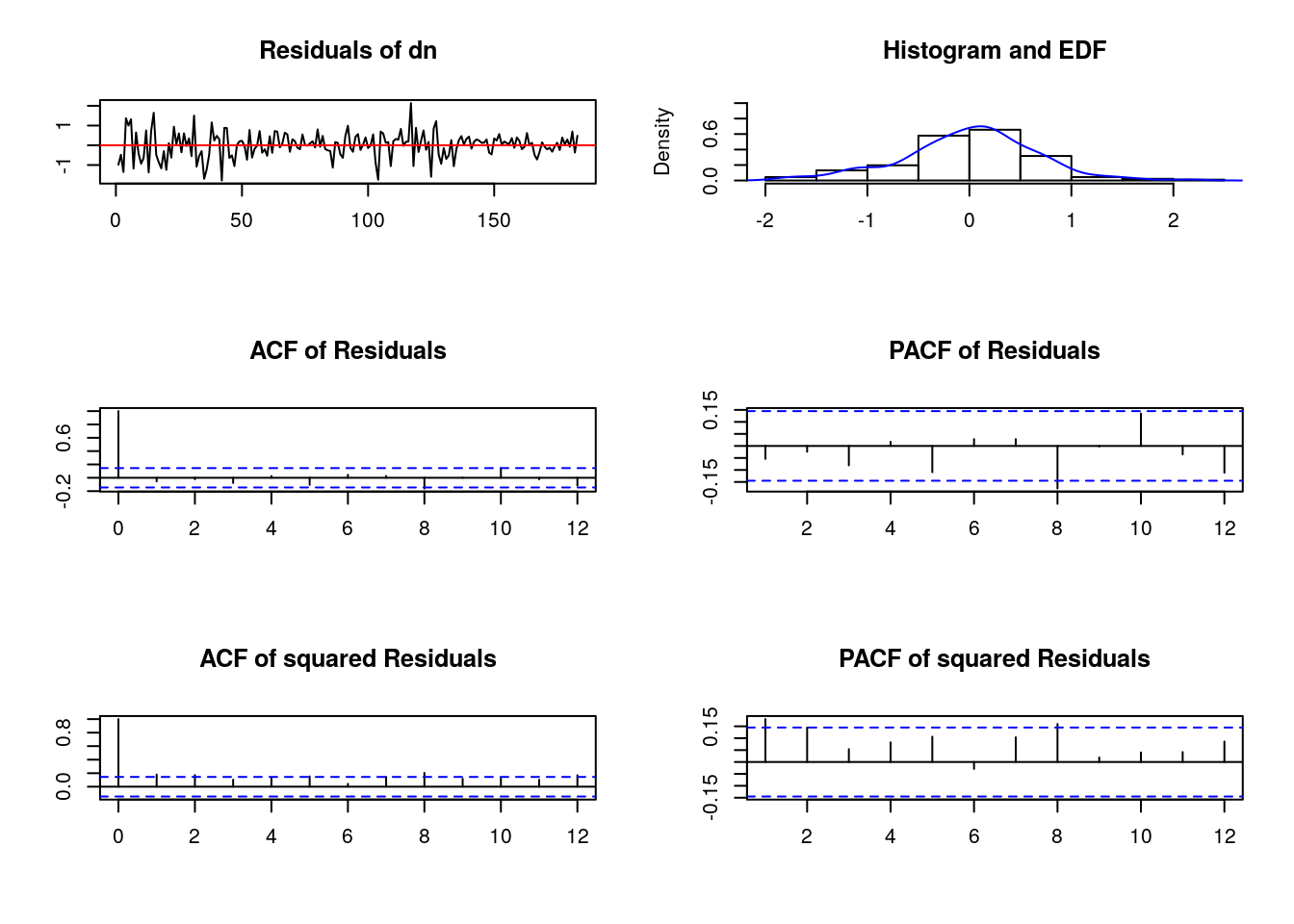
Chi-squared = 59.109, df = 2, p-value = 1.461e-13


  1. “Plotting” our “residuals test”




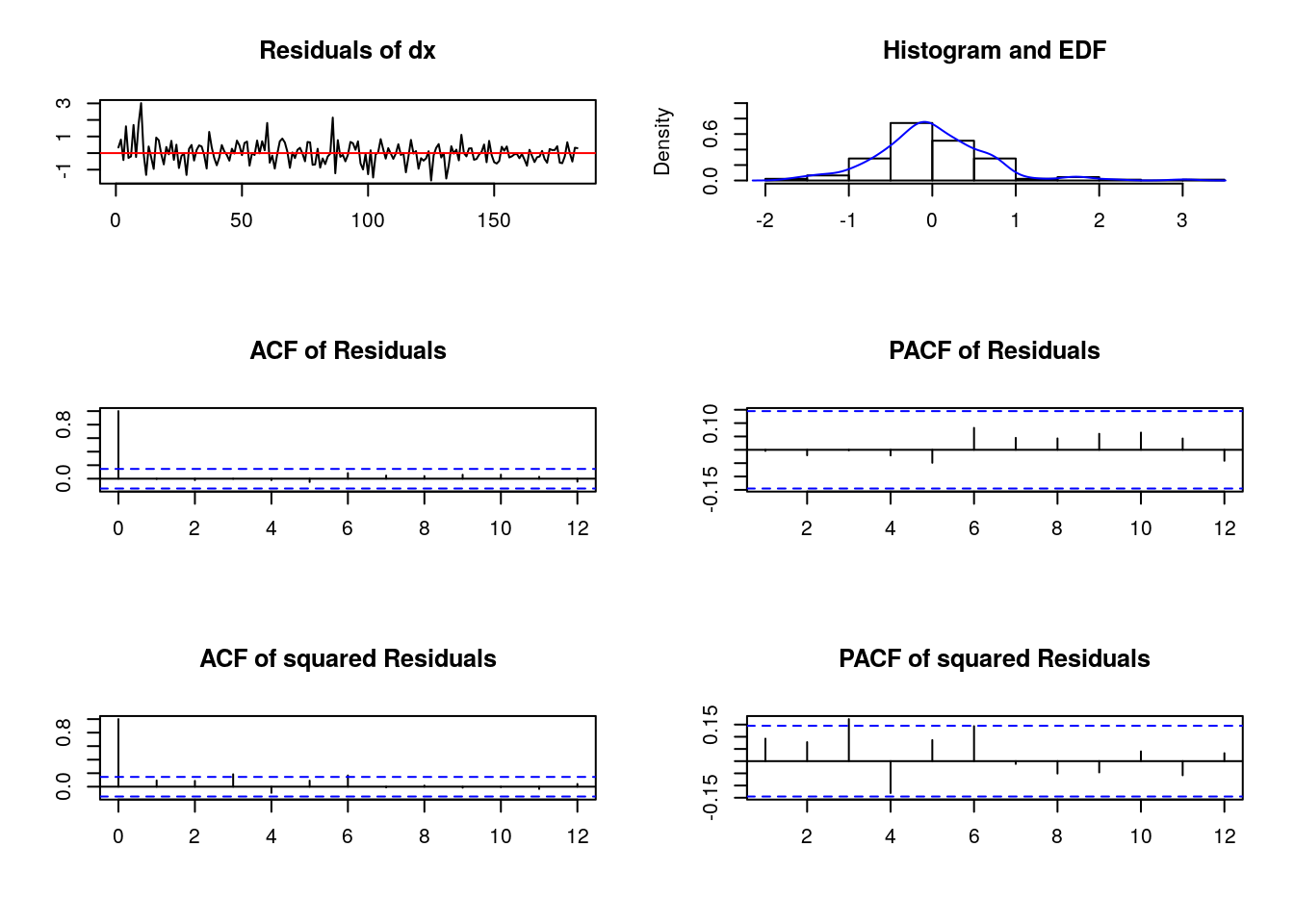
3. VAR in reduced form (Uses)


The two principal uses of VAR models in reduced form are testing (causality testing) and forecasting, BUT the most used instruments in the VAR methodology are IRF & FEVD.

IRF & FEVD only have a clear meaning if we transform our reduced form VAR model to an structural VAR. We will develop this idea in a while


Testing in a VAR

  • After validation, the VAR could be used for testing, for example, for testing Granger causality

  • As we said, if the residuals are normally distributed (Gaussian) like (\(v_{t}\rightarrow N(0,\Sigma _{v})\)) the OLS estimator has desirable asymptotic properties. In particular, it will be asymptotically normally distributed, and then, if the VAR is stable, usual inference procedures are asymptotically valid: t-statistics could be used for inference about individual parameters and F-test for testing hypothesis for sets of parameters.


Granger causality


  • Granger causality: Granger called a variable X causal for Y if the information in past and present values of X is helpful for improving the forecast of Y. If Granger causality holds, this does not guarantee that X causes Y. But, it suggests that X might be causing Y.

  • In the context of VAR models, if we want to test for Granger-causality, we need to test zero constraints in some of the coefficients.

  • Sometimes econometricians use the shorter terms causes as shorthand for Granger causes. You should notice, however, that Granger causality is not causality in a deep sense of the word. It just talk about linear prediction, and it only has “teeth” if we only find Granger causality in one direction.

  • The definition of Granger causality did not mention anything about possible instantaneous correlation between variables. If the innovations are correlated we will say that there exits instantaneous causality

  • It’s possible to test Granger causality through Wald or F-test. In the vars package:

    • It uses F-test to test Granger causality

    • Wald test for instantaneous Granger causality (non zero correlation among the \(v_{it}\))


$Granger

    Granger causality H0: dx do not Granger-cause dn

data:  VAR object our_var
F-Test = 4.6524, df1 = 4, df2 = 348, p-value = 0.001138


$Instant

    H0: No instantaneous causality between: dx and dn

data:  VAR object our_var
Chi-squared = 3.5873, df = 1, p-value = 0.05822
$Granger

    Granger causality H0: dn do not Granger-cause dx

data:  VAR object our_var
F-Test = 5.407, df1 = 4, df2 = 348, p-value = 0.0003106


$Instant

    H0: No instantaneous causality between: dn and dx

data:  VAR object our_var
Chi-squared = 3.5873, df = 1, p-value = 0.05822


Forecasting

  • We are not going to develop this topic, but… a VAR could also be used for forecasting
$dx
          fcst      lower    upper       CI
[1,] 0.3691718 -0.9506215 1.688965 1.319793
[2,] 0.1583605 -1.1744143 1.491135 1.332775
[3,] 0.2929821 -1.1194967 1.705461 1.412479

$dn
          fcst      lower    upper       CI
[1,] 0.8210940 -0.4841807 2.126369 1.305275
[2,] 0.5611573 -1.0605790 2.182894 1.621736
[3,] 0.5069927 -1.1949360 2.208921 1.701929


4. VMA represesentation


  • A stationary (stable) VAR could be transformed (inverted) in an infinite MA(\(\infty\)) process

  • By inverting the autoregressive polynomial A(L) we can obtain the VMA form of a VAR like:

\[y_{t}~=C_{0}v_{t}+C_{1}v_{t-1}+C_{2}v_{t-2}+\ ...\ [3]\]

Being \(C_{0}=I_{K}\), the rest of the \(C_{s}\) matrices could be computed recursively


  • As with the VAR, model \([3]\) can be written using a polynomial in the lag operator as:

\[y_{t}=C(L)v_{t}\ \ \ \ \ \ \ \ \ \ \ \ [4]\]

being \(C(L)=(I_{K}+C_{1}L^{1}+C_{2}L^{2}+\ \ ...)\).


  • Model \([3]\) or \([4]\) are also called the Wold VMA representation


Obtaining the VMA with R


First, test’s do it by hand (but with a little help from R).

  1. we could obtain the \(A_{i}\) matrices of the estimated VAR with the Acoef() function


  1. To obtain the Wold VMA representation of the VAR we have to invert the \(A(L)\) polynomial. We will do it by hand and also by using the vars package


2a) By hand: we could obtain the VMA matrices, the \(C_{i}\), with R with the Psi() function; but by hand it would be as:

  • \(C_{0}=I_{K}\),

  • the rest of the \(C_{s}\) matrices could be computed recursively as

\[C_{s}=\underset{j=1}{\overset{s}{\sum }}C_{s-j}A_{j}\]



2b) Using the vars package: we have to use the Phi() function

, , 1

     [,1] [,2]
[1,]    1    0
[2,]    0    1

, , 2

            [,1]       [,2]
[1,] -0.09639832 -0.1181884
[2,]  0.30492251  0.7148050

, , 3

          [,1]       [,2]
[1,] 0.1483909 -0.3049207
[2,] 0.2427883  0.3467704

, , 4

            [,1]        [,2]
[1,] -0.09808845 -0.08348028
[2,]  0.19891831  0.15758298



Let’s check if our calculation by hand coincide with the one obtained using the vars package. Our (by hand) CC2 matrix is:

         dx.l1      dn.l1
[1,] 0.1483909 -0.3049207
[2,] 0.2427883  0.3467704



5. Uses of VAR: “Structural” analysis


  • The two principal instruments of VAR’s, IRF & FEVD, are defined in terms of their VMA representation [3]

  • IRF & FEVD will show the effects of a shock, BUT in order to have a clear meaning, they must be interpreted under the assumption that all the other shocks are held constant; however, in the Wold representation the shocks are not orthogonal; that’s why we will turn our attention to the Structural VAR models


IRFs


  • Usually the main interest in VAR modelling is to look at the dynamic effect of a shock on the variables of interest

  • This dynamic effect could be easily obtained through the VMA representation [3] of the VAR

  • In particular the response of the variable \(y_{n}\) to an impulse of size one in \(v_{m}\) \(j\)-periods ahead is given by the \((n,m)\)-th element of \(C_{j}\). That is, the matrices \(C_{i}\) contain the responses of the variables to the innovations for different periods (or steps) ahead

BUT…

  • BUT, usually the VAR disturbances (or innovations) are correlated, then the interpretability of the impulse responses to innovation becomes problematic: if the innovations are correlated (off diagonal elements of \(\Sigma _{v}\) different from zero) then, an impulse in \(v_{m}\) would be associated with impulses in innovations at the other equations of the VAR model.


Sims proposal: Cholesky decomposition

  • Therefore, Sims proposed to assume recursive contemporaneous interactions among variables, i.e. imposing a certain structural ordering in the variables. In terms of the MVA representation this means that the transformed or “structural” shocks will not affect to the preceding variables instantaneously.


  • In practice, imposing a recursive contemporaneous order among the variables of the VAR model, is operationalised performing a Cholesky decomposition in \(\Sigma _{v}\).

  • The Cholesky factor, \(P\), of \(\Sigma _{v}\) is defined as the unique lower triangular matrix such that \(PP^{^{\prime }}=\Sigma _{v}\)


  • With the Cholesky factor(\(P\)) we could transform the VAR in [3] as:

\[A(L)y_{t}=PP^{-1}v_{t}\]

with \(\varepsilon _{t}=P^{-1}v_{t}\), then our transformed VAR becomes

\[A(L)y_{t}=P\varepsilon _{t}\ \ \ \ \ \ \ \ \ \ \ \ [2*]\]


  • That is, we have written our VAR in terms of a new vector of shocks \(\varepsilon _{t}\), with identity covariance matrix (\(\Sigma _{\varepsilon }=I\))

  • Now, as the \(\varepsilon _{t}\) shocks are uncorrelated their IRF would have a clear interpretation


Obtaining IRFs with R


  • From [2*] we can obtain the VMA representation in terms of the \(\varepsilon _{t}\) shocks:

\[y_{t}=C(L)P\varepsilon _{t}\ \ \ \ \ \ \ \ \ \ \ \ [5\ast ]\]

\[y_{t}=D(L)\varepsilon _{t}\ \ \ \ \ \ \ \ \ \ \ \ [5]\]

being \(D(L)=C(L)P\) ,

\(D(L)=(D_{0}+D_{1}L^{1}+D_{2}L^{2}+D_{3}L^{3}-\ \ ...)\), with \(D_{i}=C_{i}P\) ,

then \(D_{0}=C_{0}P=I_{N}P=P\)

  • As \(D_{0}=P\), and P is lower triangular, the system is recursive: the first shock (\(\varepsilon _{t}^{1}\)) could have an instantaneous effect on all the variables of the VAR, while the first variable in the VAR could only be affected contemporaneously by \(\varepsilon _{t}^{1}\)

  • The matrices \(D_{i}\) contains the response of the variables to the \(\varepsilon _{t}\)

  • In particular the response of the variable \(y_{n}\) to an impulse of size one in \(\varepsilon_{m}\) \(j\)-periods ahead is given by the \((n,m)\)-th element of \(D_{j}\).

  • Don’t worry too much now because firstly we will usually do this with R and secondly because we are going to practice the calculations by hand at the Lab, but ….

  1. To obtain the orthogonalised IRF (the \(D_{i}\) matrices), the matrices with the IRFs
  • First we have to obtain the Cholesky factor P as \(PP^{^{\prime }}=\Sigma _{v}\)
  • Latter, we have to calculate the \(D_{i}=C_{i}P\) matrices

3a) By hand

3b) We have to use the Psi() function (Note that the function is Psi(), not the previous Phi() ) function

, , 1

            [,1]      [,2]
[1,]  0.67337627 0.0000000
[2,] -0.09417032 0.6592771

, , 2

           [,1]        [,2]
[1,] -0.0537825 -0.07791893
[2,]  0.1380142  0.47125458

, , 3

          [,1]       [,2]
[1,] 0.1286374 -0.2010272
[2,] 0.1308324  0.2286178

, , 4

            [,1]        [,2]
[1,] -0.05818907 -0.05503664
[2,]  0.11910723  0.10389086

Let’s check our DD3 with the calculations made with the var package.

              dx          dn
[1,] -0.05818907 -0.05503664
[2,]  0.11910723  0.10389086


  • Let’s show again the (Cholesky) IRF, but in the usual form:

Impulse response coefficients
$dx
               dx          dn
[1,]  0.673376268 -0.09417032
[2,] -0.053782498  0.13801416
[3,]  0.128637414  0.13083241
[4,] -0.058189069  0.11910723
[5,]  0.005719843  0.12022354
[6,] -0.036212427  0.06355445
[7,] -0.020107696  0.01886216


  • In fact, usually IRF’s are shown in graphical form:




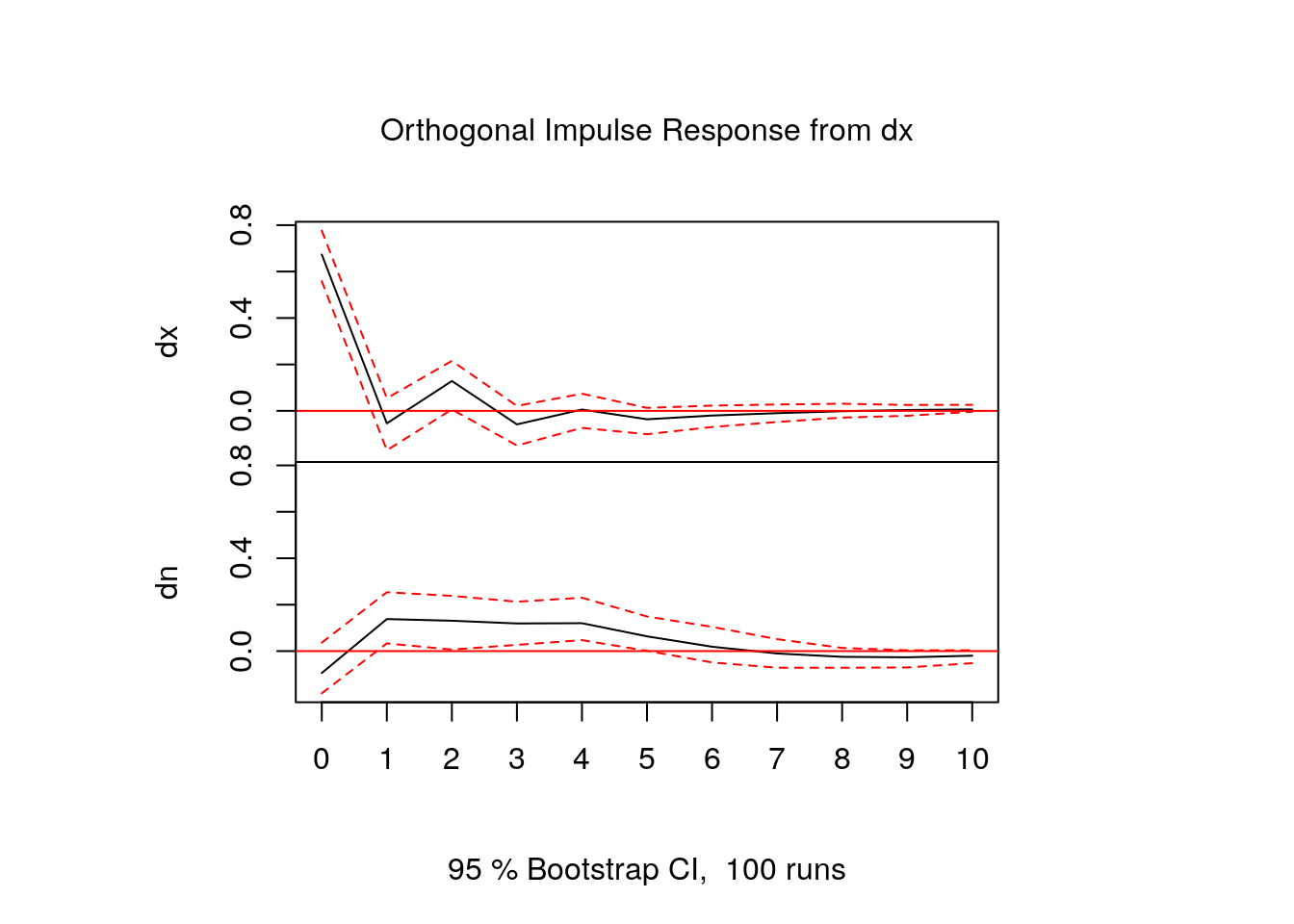
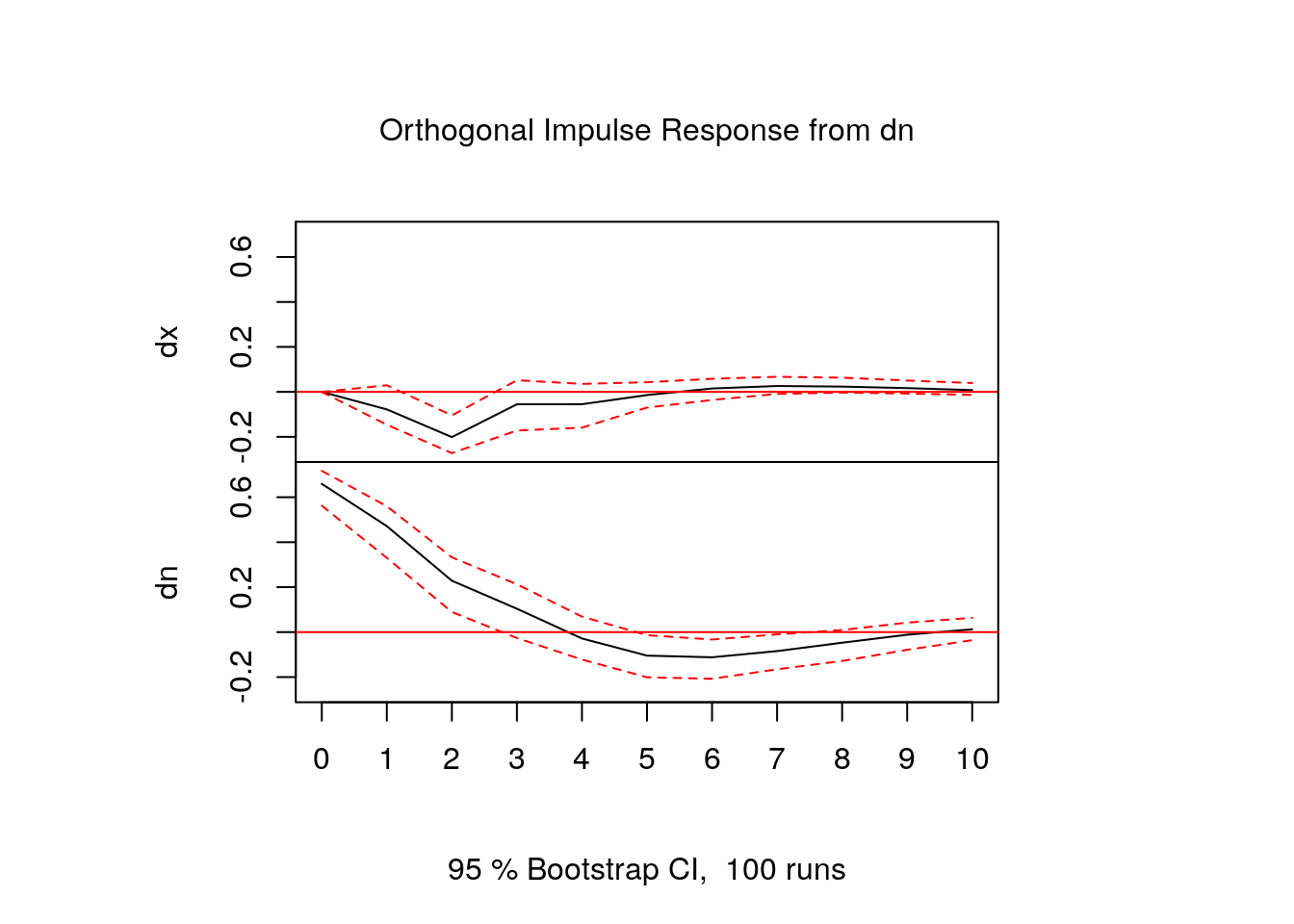
FEVD


  • FEVD : Forecast error variance decomposition

  • Once we have orthogonalised IRF’s (the \(D_{i}\) matrices ), the FEVD can be easily computed. Let’s see how:


  • The h-step forecast error can be represented as:

\[y_{T+h}-y_{T+h\mid T}=D_{0}\varepsilon _{T+h}+D_{1}\varepsilon_{T+h-1}+\cdots +D_{h-1}\varepsilon _{T+1}\]

As \(\Sigma _{\varepsilon }=I\), the forecast error variance of the k-th component of \(y_{T+h}\) is:

\[\sigma _{k}^{2}(h)=\overset{h-1}{\underset{j=0}{\sum }}(d_{k1,j}^{2}+\cdots +d_{kK,j}^{2})=\overset{K}{\underset{j=1}{\sum }}(d_{kj,0}^{2}+\cdots +d_{kj,h-1}^{2})\]

where \(d_{nm,j}\) denotes the \((n,m)-th\) element of \(D_{j}\).


  • The quantity \((d_{kj,0}^{2}+\cdots +d_{kj,h-1}^{2})/\sigma _{k}^{2}(h)\) represents the contribution of the \(j\)-th shock to the h-step forecast error variance of variable \(k\).

  • Don’t worry too much now because firstly we will usually do this with R and secondly because we are going to practice the calculations by hand at the Lab, but ….


The FEVD are obtained through the IRF. Let’s see the FEVD and we will calculate it latter by hand:


$dx
            dx         dn
[1,] 1.0000000 0.00000000
[2,] 0.9868699 0.01313012
[3,] 0.9104987 0.08950130
[4,] 0.9058296 0.09417038
[5,] 0.9007024 0.09929755
[6,] 0.9006125 0.09938748

$dn
             dx        dn
[1,] 0.01999496 0.9800050
[2,] 0.04077447 0.9592255
[3,] 0.05972348 0.9402765
[4,] 0.07601943 0.9239806
[5,] 0.09275743 0.9072426
[6,] 0.09603517 0.9039648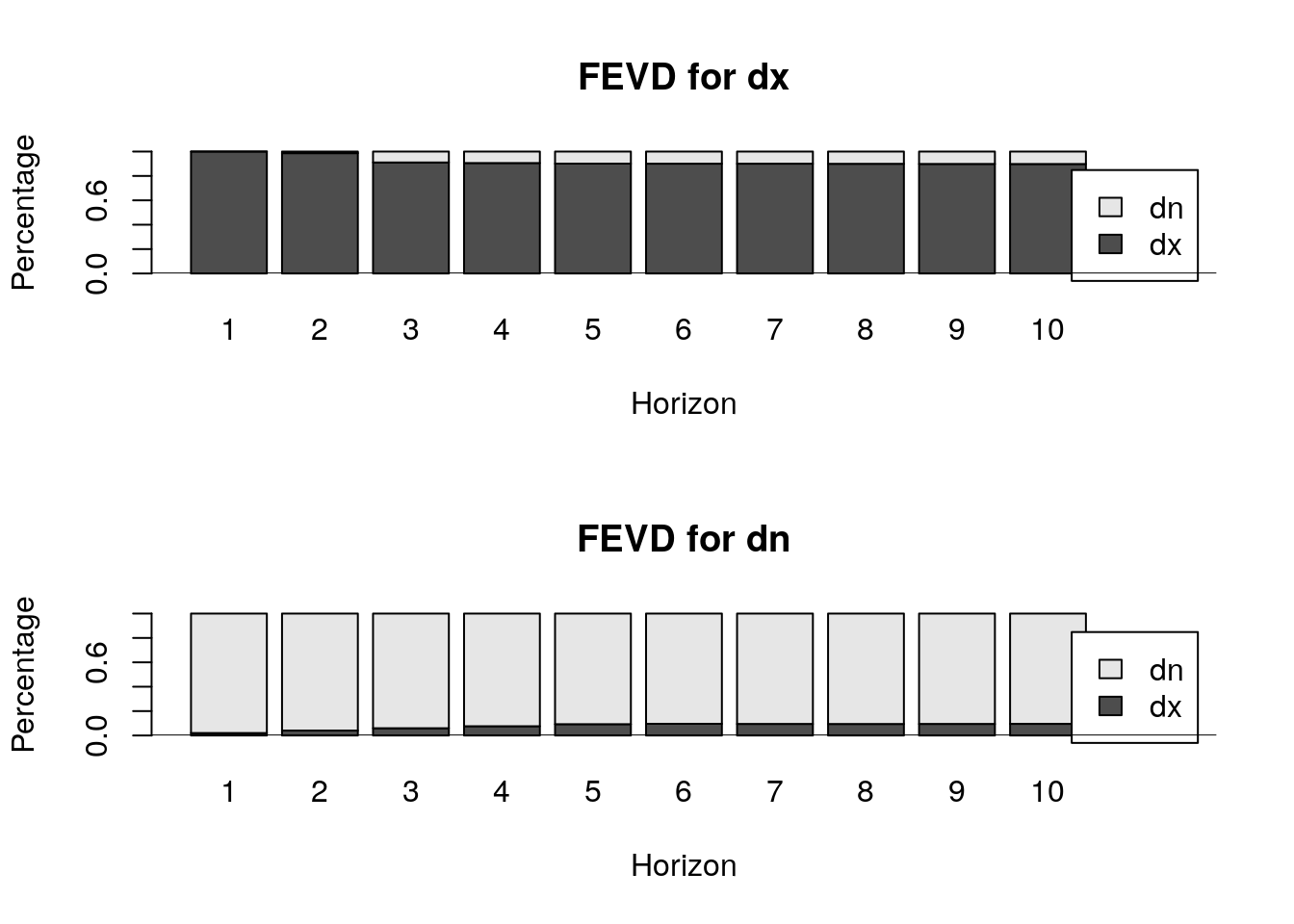


Looking at the relation among IRF and FEVD


  • To obtain the IRF’s we have to use the irf() function



Impulse response coefficients
$dx
              dx
[1,]  0.67337627
[2,] -0.05378250
[3,]  0.12863741
[4,] -0.05818907

$dn
              dx
[1,]  0.00000000
[2,] -0.07791893
[3,] -0.20102724
[4,] -0.05503664


  • To obtain the FEVD we have to use the fevd() function


fevd() function to calculate the FEVD

$dx
            dx         dn
[1,] 1.0000000 0.00000000
[2,] 0.9868699 0.01313012
[3,] 0.9104987 0.08950130
[4,] 0.9058296 0.09417038

$dn
             dx        dn
[1,] 0.01999496 0.9800050
[2,] 0.04077447 0.9592255
[3,] 0.05972348 0.9402765
[4,] 0.07601943 0.9239806


  • To illustrate how to obtain the FEVD by hand, let’s first look inside the object our_irfs who will contain the IRF’s of our_var:


[1] "varirf"


  • With class(our_irfs) we have seen that our_irfs is an object of class “varirf”. Pfaff defined this type of object to allocate space to save the IRF’s

  • OK, our_irfs is an object of class “varirf, but with str(our_irfs) we can look at the internal structure of the object”our_irfs" and we can see that in fact is a list of 13 elements. Too many for our purposes, then let’s concentrate only in the first element that contains the true IRF.

  • Let’s save the first element of our_irfs to look inside again


List of 2
 $ dx: num [1:6, 1:2] 0.67338 -0.05378 0.12864 -0.05819 0.00572 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : NULL
  .. ..$ : chr [1:2] "dx" "dn"
 $ dn: num [1:6, 1:2] 0 -0.0779 -0.201 -0.055 -0.0547 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : NULL
  .. ..$ : chr [1:2] "dx" "dn"


  • we can see that our_IRF1 is a list with 2 elements. The first one our_IRF1[[1]] contains the responses of the first variable to the two shocks. The second our_IRF1[[2] contains the responses of the second variable to the two shocks

  • Let’s concentrate only on the movement (or responses) of the first variable (dx). The FEVD of the first variable is calculated as:



  • Let’s see, step by step, what we have done:


[1]  0.673376268 -0.053782498  0.128637414 -0.058189069  0.005719843
[1]  0.00000000 -0.07791893 -0.20102724 -0.05503664 -0.05474057
[1] 0.000000000 0.006071360 0.040411950 0.003029032 0.002996530
[1] 0.00000000 0.00607136 0.04648331 0.04951234 0.05250887



  • Checking if we have calculated the FEVD correctly:


[1] 1.0000000 0.9868699 0.9104987 0.9058296
[1] 0.00000000 0.01313012 0.08950130 0.09417038
$dx
            dx         dn
[1,] 1.0000000 0.00000000
[2,] 0.9868699 0.01313012
[3,] 0.9104987 0.08950130
[4,] 0.9058296 0.09417038

$dn
             dx        dn
[1,] 0.01999496 0.9800050
[2,] 0.04077447 0.9592255
[3,] 0.05972348 0.9402765
[4,] 0.07601943 0.9239806


  • OK, we know already how to estimate-validate-use a VAR in reduced form & to obtain and interpret the Cholesky IRF & FEDV.


  • In the next Lab we will illustrate other ways to identify a SVAR